Las funciones cuadráticas son más
que curiosidades algebraicas — son ampliamente usadas en la ciencia, los
negocios, y la ingeniería. La parábola con forma de U puede describir
trayectorias de chorros de agua en una fuente y el botar de una pelota, o
pueden ser incorporadas en estructuras como reflectores parabólicos que forman
la base de los platos satelitales y faros de los carros. Las funciones
cuadráticas ayudan a predecir ganancias y pérdidas en los negocios, graficar el
curso de objetos en movimiento, y asistir en la determinación de valores
mínimos y máximos.
Comúnmente usamos ecuaciones
cuadráticas en situaciones donde dos cosas se multiplican juntas y ambas
dependen de la misma variable. Por ejemplo, cuando trabajamos con un área. Si
ambas dimensiones están escritas en términos de la misma variable, usamos una
ecuación cuadrática. Porque la cantidad de un producto vendido normalmente
depende del precio, a veces usamos una ecuación cuadrática para representar las
ganancias como un producto del precio y de la cantidad vendida. Las ecuaciones
cuadráticas también son usadas donde se trata con la gravedad, como por ejemplo
la trayectoria de una pelota o la forma de los cables en un puente suspendido.
Usando
la Parábola
Una aplicación muy común y fácil
de entender de una función cuadrática es la trayectoria seguida por objetos
lanzados hacia arriba y con cierto ángulo. En estos casos, la parábola
representa el camino de la pelota (o roca, o flecha, o lo que se haya lanzado).
Si graficamos la distancia en el eje x y la altura en el
eje y, la distancia que del lanzamiento será el valor de x cuando y es
cero. Este valor es una de las raíces de una ecuación cuadrática, o intersecciones en x, de la parábola. Sabemos cómo encontrar las raíces
de una ecuación cuadrática — ya sea factorizando, completando el cuadrado, o
aplicando la fórmula cuadrática.
Otro uso común de las ecuaciones
cuadráticas en aplicaciones del mundo real es encontrar el valor máximo (el
mayor o más alto) o el mínimo (el menor o más bajo) de algo. Recuerda que el
vértice es el punto donde una parábola da la vuelta. Para una parábola que abre
hacia abajo, el vértice es el punto más alto, lo que ocurre al máximo valor
posible de y. Para una parábola que abre hacia abajo, el vértice es
el punto más bajo de la parábola, y ocurre al mínimo valor de y.
Para encontrar el máximo o el
mínimo con una ecuación cuadrática, usualmente queremos poner la ecuación
cuadrática en su forma vértice de una ecuación
cuadrática,
Esto nos permite rápidamente
identificar las coordenadas del vértice (h, k).
Veamos cómo funciona esto con un
problema de movimiento. La ecuación
es comúnmente usada para
modelar un objeto que ha sido lanzado o aventado. La
variable h representa la altura en pies, y t representa
el tiempo en segundos. Los otros dos valores son números generalmente
dados: h0 es la altura inicial en pies y v0 es
la velocidad inicial en pies/segundo.
Cuando trabajamos con
esta ecuación, asumimos que el objeto está en "caída libre", lo que
significa que se mueve sólo bajo la influencia de la gravedad. No hay resistencia
contra el aire u otra interferencia de ningún tipo (no tan parecido al mundo
real, pero de todos modos, estas ecuaciones son útiles).
Pudimos
haber encontrado el vértice usando otros métodos, por ejemplo graficando o
usando la fórmula
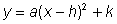
Recomiendo algún dibujo.
ResponderBorrar